* 문제 링크
https://www.acmicpc.net/problem/11375
11375번: 열혈강호
강호네 회사에는 직원이 N명이 있고, 해야할 일이 M개가 있다. 직원은 1번부터 N번까지 번호가 매겨져 있고, 일은 1번부터 M번까지 번호가 매겨져 있다. 각 직원은 한 개의 일만 할 수 있고, 각각
www.acmicpc.net
문제 내용 요약
강호네 회사에서는 직원 N명과 할 일 M개가 있다. (1 ≤ N,M ≤ 1000)
직원 한 명은 한 개의 일만 가능하고, 한 일에는 한 명만 배정되어야 한다.
최대 몇 개의 일을 할 수 있을까?
접근법
하나의 직원에 하나의 일을 매칭하는, 즉 2개의 집합의 원소를 일대일로 매칭시키는 문제다.
가장 기본적인 "이분 매칭(Bipartite Matching)" 문제라고 할 수 있다.
그래서 이 아래의 설명은 이분 매칭에 대한 설명 위주로 이루어질 것이다.
5 5
2 1 2
1 1
2 2 3
3 3 4 5
1 1
위의 케이스 (예제 입력이다) 를 기준으로 설명하도록 하겠다.
무엇을 의미하는지는 문제 링크를 통해 보고 오기를 바란다.
일단은 두 개의 집합으로 나누는 것이 먼저다.
별 문제없이 그냥 직원 집합, 일 집합으로 나누면 된다.

그리고 연결시켜보자

앞에 S(start) 노드에서 모든 직원 노드로 뻗어나가는 연결,
뒤에는 모든 일 노드에서 E(end) 노드로 뻗어나가는 연결이 추가되어 있는 그림들이 많다.
그래서 S→(직원)→(일)→E 로 뻗어나가는 네트워크 플로우로 설명하곤 하지만,
지금 이 문제를 푸는 데에 있어 오히려 직접적으로 안 쓰다보니 사족이 될 수 있어서 특별히 추가하지는 않겠다.
이제 1번 직원부터 매칭을 시켜보자.
1번째 일부터 할 수 있는지 확인하면서 진행할 것이다.

일단 1번 일을 맡은 직원이 없어 1번 직원과 1번 일을 매칭해주고, 매칭 가능하다는 뜻의 true를 반환한다.
그리고 일에 매칭된 직원의 번호를 저장해둔다.
앞으로 초록색 화살표는 매칭 완료, 보라 화살표는 매칭되는지 확인 진행중이라 생각하면 된다.

이제 2번 직원이 1번 일을 보는데, 1번 일이 지금 1번 직원에 매칭되어있다.

그래서 1번 직원은 2번 일을 할 수 있는지 확인해본다.
2번 일에 매칭된 직원이 없기 때문에, 1번 직원과 2번 일을 매칭 및 저장해주고, true 를 반환한다.
1번 직원과 매칭되었던 1번 일은 이제 2번 직원과 매칭이 될 수 있다는 신호를 받았기 때문에
2번 직원과 매칭해주고, 저장, true를 반환한다.

대충 이런 식으로, 직원과 일을 매칭시킬 때,
1. 일을 맡은 직원이 없으면 해당 일과 직원을 매칭한다. (true를 반환)
2. 일을 맡은 직원이 이미 있으면, 그 직원이 다른 일과 매칭할 수 있는지 확인해주는 작업을 재귀적으로 실행한다.
2-1. 다른 일과 매칭이 가능할 경우, true를 반환하며
해당하는 직원과 일을 다시 매칭해주는 작업을 재귀적으로 실행한다.
2-2. 다른 일과 매칭이 불가능할 경우, false를 반환하며 재매칭을 해주지 않고 그대로 가도록 한다.
이와 같이 깊이 우선 탐색(DFS)과 같은 방식으로 가능한지 검색을 해주어 매칭을 시켜주면 된다.
나머지는 아래와 같이 진행될 것이다.
 3번 직원→3번 일 매칭 가능, 매칭 완료 |
 4번 직원→3번 일 매칭 검색 |
 3번 일과 매칭되었던 3번 직원과 2번 일의 매칭 검색 |
 2번 일과 매칭되었던 1번 직원과 1번 일의 매칭 검색 |
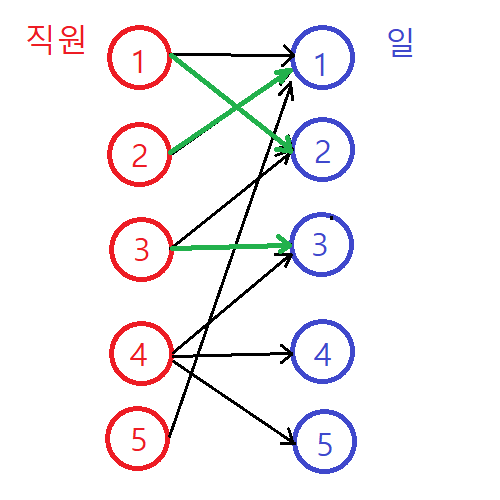 1번 일과 매칭되었던 2번 직원 검색 매칭 불가능 확인 후 되돌아오기 |
 4번 직원→4번 일 매칭 가능, 매칭 완료 |
4번 직원의 경우와 같이, 매칭이 불가능한 방법이라면,
되돌아와서 다른 매칭을 시도한다. 보통은 1번부터 하는 것이 편한데,
무작위로 시도한다고 해도 안될 것은 없긴 하다.
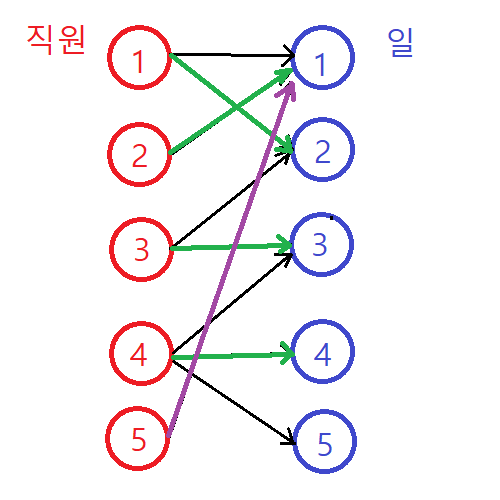 5번 직원→1번 일 매칭 검색 |
 1번 일과 매칭되었던 2번 직원 검색, 매칭 불가능. 최종적으로 5번 직원은 매칭 불가능 |
위의 방법으로, 4라는 답을 도출해낼 수 있다.
이렇게 "이분 매칭"을 배워봤는데, 시간 복잡도는 결국 매칭의 검색량에 비례하게 된다.
검색량은 정점(직원과 일 수)과 간선(어떤 직원이 어떤 일을 할 수 있는지 수) 수에 영향을 받는데,
간선마다 정점의 개수만큼 검색될 수 있기 때문에,
시간 복잡도는 O(VE) (V = 정점의 갯수, E = 간선의 갯수) 이다.
작성한 코드에 따라 V가 이 문제에서 N 또는 M 이 될 것이니, 참고하길 바란다.
내 코드
#include <iostream>
#include <vector>
#include <cstring>
using namespace std;
vector<int> emp[1010];
int emp_to_work[1010];
int work_to_emp[1010];
bool vstd[1010];
bool work(int a) {
if(vstd[a]) return false;
vstd[a]=1;
for(int b:emp[a]) {
if(work_to_emp[b]==0||work(work_to_emp[b])) {
emp_to_work[a]=b;
work_to_emp[b]=a;
return true;
}
}
return false;
}
int main() {
int n,m,s=0;
cin>>n>>m;
for(int i=1;i<=n;i++) {
int t;
scanf("%d",&t);
for(int j=0;j<t;j++) {
int u;
scanf("%d",&u);
emp[i].push_back(u);
}
}
for(int i=1;i<=n;i++) {
memset(vstd,0,sizeof(vstd));
if(work(i)) s++;
}
cout<<s;
}필요없는 메모리(emp_to_work)가 존재하지만, 학습을 위해서 남겨둔 흔적이니 없애도 된다.
여담
이 문제는 네트워크 플로우 문제로 풀 수도 있는데,
이분 매칭이 조금 더 특화된 형태고, 코드로 짜기도 쉽다고 생각한다.
그래서 이분 매칭 쓸 수 있는 문제면 쉽게쉽게 써먹자.
'개발일지 > Problem Solving' 카테고리의 다른 글
| 백준 11053번 - 가장 긴 증가하는 부분 수열 (LIS) (0) | 2023.02.03 |
|---|---|
| 백준 11376번 - 열혈강호 2 (0) | 2023.01.30 |
| 백준 3878번 - 점 분리 (0) | 2023.01.24 |
| 백준 17387번 - 선분 교차 2 (0) | 2023.01.19 |
| 백준 3679번 - 단순 다각형 (2) | 2023.01.18 |

