* 문제 링크
https://www.acmicpc.net/problem/10254
10254번: 고속도로
n개의 도시를 가진 나라가 있다. 이 나라에서는 도시들 중 가장 먼 두 도시 사이에 직행 고속도로를 놓으려 한다. 고속도로는 시작점과 끝점이 아닌 다른 나라를 통과해도 된다. 즉, n개의 도시
www.acmicpc.net
문제 내용 요약
나라에 도시 N개 (2 ≤ N ≤ 200,000) 가 있는데
거기에서 가장 먼 두 도시를 찾아내라.
접근법
이 문제는 회전하는 캘리퍼스 (Rotating Calipers) 를 사용하기 때문에,
컨벡스 헐을 기본으로 깔고 가야한다.
컨벡스 헐에 대한 설명 및 내용은 아래 글 참조
백준 1708번 - 볼록 껍질
* 문제 링크 https://www.acmicpc.net/problem/1708 1708번: 볼록 껍질 첫째 줄에 점의 개수 N(3 ≤ N ≤ 100,000)이 주어진다. 둘째 줄부터 N개의 줄에 걸쳐 각 점의 x좌표와 y좌표가 빈 칸을 사이에 두고 주어진다
syerco0.com
회전하는 캘리퍼스를 사용하려면 먼저 컨벡스 헐을 구해야 한다.
왜?
일단 이게 캘리퍼스다.

아마 웬만하면 다들 알고, 어떤 용도고, 어떻게 사용하는지 알 것이다.
물체에다가 저 튀어나온 부분을 조여서 길이를 측정하는 그거다.
그렇다! 캘리퍼스는 물체의 겉부분을 돌리고 돌려서(?) 길이를 구한다.
그러면 이제 대충 감이 올 것이다.
컨벡스 헐을 구하고나서 돌돌 돌리면서 길이를 구해주고, 그 중에 최대인 걸 건지면 된다.
위의 글을 통해 어찌되었든 컨벡스 헐을 구하는 방법을 알았을테니,
돌돌 돌리면서 캘리퍼스로 길이를 구하는 방법을 알아보자.

당연하지만 진짜 캘리퍼스처럼 일일이 각도를 조금씩 조금씩 돌려가면서 길이를 구할 수는 없다.
대신 비슷한 느낌으로 길이를 잴 두 점을 선택할 수 있다.
캘리퍼스의 길이를 재는 튀어나온 부분은 평행이다.
비슷한 느낌으로, 최대한 평행하게 놓일 수 있는 점들을 선택하면 된다.
무슨 소리인지 모르겠나? 솔직히 나도 그렇다. 이게 무슨 소리야

위 그림의 검은 원이 있는 꼭짓점부터 시작해보자.
첫번째 점(빨간 점), 두번째 점(녹색 점)을 가지고 먼저 길이를 구해준다.
누가봐도 겁나 짧지만 일단 구해준다. 길이를 구하는 방법은 알고 있을 것이라 믿는다.
모른다면 이 문제를 풀 때가 아닐지도 모르겠다. 공부합시다.
그 다음으로 선택해줄 두 점을 골라보자.
어떻게 고를까?

1번 점, 2번 점, 3번 점 순서로 CCW 를 구하자.
CCW를 잘 알고 있다면, 지금 상황이 1이라는 것을 알 수 있다.
일단 다음과 같이 한다고 주입하자.
CCW가 0 이상이면 초록색 점을 다음 점으로 바꾸고, 음수면 빨간 점을 다음 점으로 바꾸자.

그리고 또 길이를 구해준다. 일단은 전보다는 길어보인다.
이제 CCW를 구해줘야되는데... 어떻게 하지?

빨간 점 다음 점 위치로 벡터(화살표)를 이동해준다고 생각하자.
그러면 대충 "구해지는 4번 점의 위치"는 "(2번 점에서 3번 점으로 가는 벡터)를 4번 점에서 뺀 위치"겠다.
그렇게 구한 점을 이용해서 CCW를 또 구해주자.
순서는 항상 중요하다. 잘못하면 CCW가 잘못 구해진다는 것은 당연하다.
아래의 그림은 내가 직접 그린 그림이다보니 대충 CCW가 그런갑다하고 넘어가자.
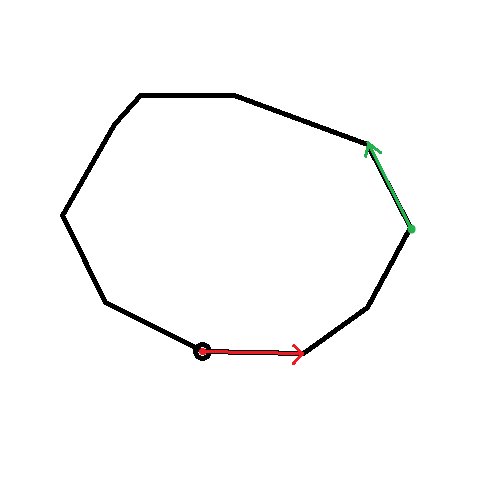 CCW > 0, 초록 이동 |
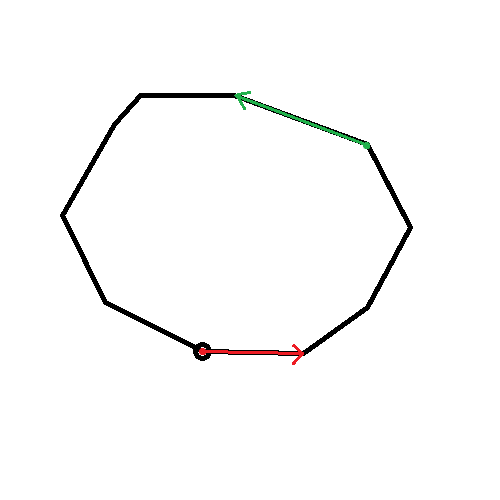 CCW > 0, 초록 이동 |
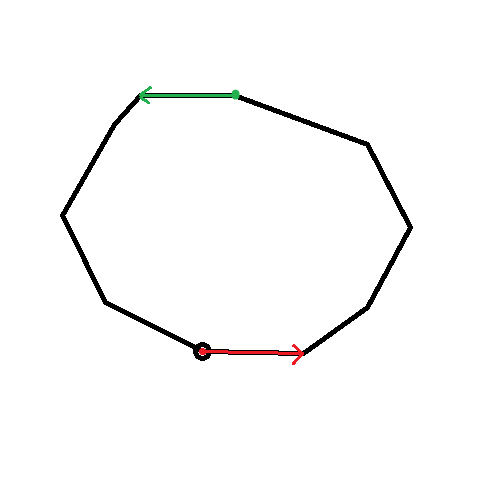 CCW < 0 (자세히 봐야됨), 빨강 이동 |
 CCW > 0, 초록 이동 |
 CCW < 0, 빨강 이동 |
 CCW > 0, 초록 이동 |
 CCW = 0, 초록 이동 |
다 하려면 힘들어서 안되겠다.
과정을 진행하다보면 마치 진짜 캘리퍼스처럼 최대한 평행한 두 화살표 위의 점 2개를 가지고
길이를 구하는 것이 진행됨을 알 수 있다.
언제 끝내면 되는가?
어차피 회전하는 캘리퍼스는 O(N) 의 시간복잡도를 가지므로 상관이 없다.
컨벡스 헐을 구할 때 정렬이 결국 O(NlogN) 이었기 때문에...
안전하게 빨간 점이 다시 처음으로 돌아올 때까지 구해주면 된다.
그동안 대충 눈대중으로 구해보면 알겠지만 (매우 성의 없는!!)

이때 제일 길다. 위의 그림들을 따라와보면 알겠지만 이 두 점이 선택되는 때가 존재한다.
그래서 결론적으로, 회전하는 캘리퍼스는 아래와 같이 실행하면 된다.
(위의 그림들을 기준으로)
빨간 점과 그 다음 점, 초록 점의 다음 점을 평행이동한 위치의 점의 CCW 값을 구해서
CCW > 0 일 때 초록 점 이동,
CCW < 0 일 때 빨간 점 이동한다.
0일 때는 원하는대로 코드를 짜준다.
(나는 초록 점 이동했다)
그렇게 길이를 구하고 그 중에 최대를 구한다.
이걸 글로 설명하기가 참 난감해서 어쩔 수 없이 위와 같은 식으로 표현함에 대해
안타까움을 표현해주시기 바랍니다. 잔짜잔
아 물론 껍질 없이 점 2개 밖에 없는 경우도 예외처리를 해줘야 함을 잊지 말자.
내 코드
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
typedef long long ll;
struct D{
ll x,y;
};
D d[200010],s[200010],mi;
ll ccw(D a,D b,D c) {
ll n=(b.x-a.x)*(c.y-a.y)-(b.y-a.y)*(c.x-a.x);
return n;
}
bool cmp(D x,D y) {
ll n=ccw(mi,x,y);
if(n==0) {
if(abs(x.x)+abs(x.y)<abs(y.x)+abs(y.y)) return 1;
return 0;
}
if(n>0) return 1;
return 0;
}
ll sql(D x,D y) {
return (y.x-x.x)*(y.x-x.x)+(y.y-x.y)*(y.y-x.y);
}
D add(D a,D b) { return D{a.x+b.x,a.y+b.y}; }
D sub(D a,D b) { return D{a.x-b.x,a.y-b.y}; }
int main() {
int t;
cin>>t;
while(t--) {
int n,mini,i;
scanf("%d",&n);
mi={99999999,99999999};
for(i=0;i<n;i++) {
scanf("%lld %lld",&d[i].x,&d[i].y);
if(mi.y>d[i].y||(mi.y==d[i].y&&mi.x>d[i].x)) mi={d[i].x,d[i].y},mini=i;
}
swap(d[0],d[mini]);
sort(d+1,d+n,cmp);
int idx=2;
s[0]=d[0];
s[1]=d[1];
for(i=2;i<n;i++) {
while(idx>1&&ccw(s[idx-2],s[idx-1],d[i])<=0) idx--;
s[idx++]=d[i];
}
ll mxl=0;
int l=0,r=1,trig=0,xa,xb;
if(idx==2) {
printf("%lld %lld %lld %lld\n",s[0].x,s[0].y,s[1].x,s[1].y);
continue;
}
while(trig==0||l!=0) {
if(mxl<sql(s[l],s[r])) {
xa=l,xb=r;
mxl=sql(s[l],s[r]);
}
if(ccw(s[l],s[(l+1)%idx],sub(add(s[(r+1)%idx],s[(l+1)%idx]),s[r]))>=0) r=(r+1)%idx;
else l=(l+1)%idx;
if(l!=0) trig=1;
}
printf("%lld %lld %lld %lld\n",s[xa].x,s[xa].y,s[xb].x,s[xb].y);
}
}'개발일지 > Problem Solving' 카테고리의 다른 글
| 백준 9663번 - N-Queen (0) | 2023.02.13 |
|---|---|
| 백준 9251번 - LCS (Longest Common Subsequence) (0) | 2023.02.08 |
| 백준 2565번 - 전깃줄 (0) | 2023.02.07 |
| 백준 11054번 - 가장 긴 바이토닉 부분 수열 (0) | 2023.02.05 |
| 백준 11053번 - 가장 긴 증가하는 부분 수열 (LIS) (0) | 2023.02.03 |


